Introduction

In previous posts, we’ve encountered the concept of tensors in GGML many times. However, we’ve only explored their simplest usage—cases without quantization, without permutation (where the tensor has a contiguous in-memory layout), and without tensor views. In more complex scenarios, tensors exhibit far more intricate behaviors, sometimes even counterintuitive ones. In this post, I’ll take a deeper dive into how tensors work in GGML.

ggml_tensor Data Structure

Overview

First, let’s take a look at the ggml_tensor data structure defined in include/ggml.h.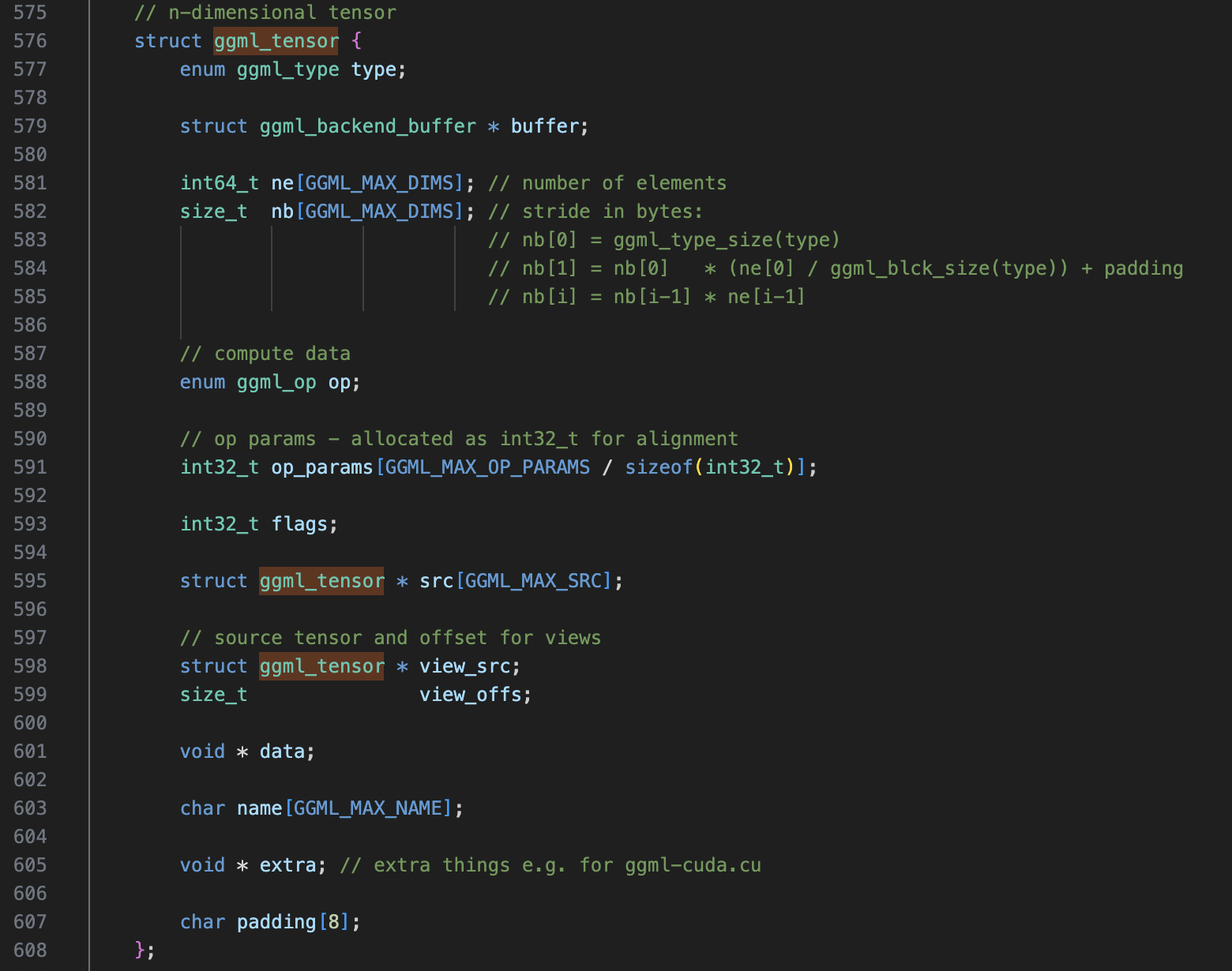

Here are some fields that you should pay attention to:

enum ggml_type type: The tensor’s data type (e.g., GGML_TYPE_F32, GGML_TYPE_Q4_0, etc.).
enum ggml_op op: The operator that produces this tensor (e.g., GGML_OP_ADD, GGML_OP_MATMUL, etc.).
char name[GGML_MAX_NAME]: The name of the tensor.
struct ggml_tensor *src[GGML_MAX_SRC]: Pointers to the parent tensors of this tensor.
struct ggml_tensor *view_src: Points to the underlying tensor if this tensor is a view of another tensor (explained later).
size_t view_offs: view offset, used together with view_src .
int32_t op_params[GGML_MAX_OP_PARAMS / sizeof(int32_t)]: Operator-specific parameters (e.g., dimension information for ggml_permute).
int64_t ne[GGML_MAX_DIMS]: Tensor shape information (important, explained later).
size_t nb[GGML_MAX_DIMS]: Strides in each dimension (important, explained later).

How to Setup a Simple Testing Environment

Simply staring at the source code won’t help much. To truly understand the internal mechanisms we’ll explore in this post, you need to set up a debugging environment to observe GGML’s runtime behavior. Here’s a minimal setup for inspecting ggml_tensor in action:

Create a new folder tensor-testunder examples/.
In examples/tensor-test,create a CMakeLists.txtwill the following content:

add_executable(tensor-test main.cpp)
target_compile_options(tensor-test PRIVATE -g)
target_compile_options(tensor-test PRIVATE -O0)
target_link_libraries(tensor-test PRIVATE ggml)

Edit examples/CMakeLists.txt, adding one line add_subdirectory(tensor-test).
In examples/tensor-test, create main.cpp , the following is a simple start point:

#include "ggml.h"
#include "ggml-cpu.h"

#include <iostream>
#include <vector>

int main () {
    struct ggml_init_params params {
        /*.mem_size   =*/ 1024 * 1024 * 1024 + ggml_graph_overhead(),
        /*.mem_buffer =*/ NULL,
        /*.no_alloc   =*/ false,
    };

    ggml_context * ctx = ggml_init(params);

    // --------------------
    // Modify this section to test different tensor computations
    float a_data[3 * 2] = {
        1, 2,
        3, 4,
        5, 6
    };

    float b_data[3 * 2] = {
        1, 1,
        1, 1,
        1, 1
    };
    
    ggml_tensor* a = ggml_new_tensor_2d(ctx, GGML_TYPE_F32, 2, 3);
    ggml_tensor* b = ggml_new_tensor_2d(ctx, GGML_TYPE_F32, 2, 3); 
    memcpy(a->data, a_data, ggml_nbytes(a));
    memcpy(b->data, b_data, ggml_nbytes(b));

    ggml_tensor* result = ggml_add(ctx, a, b);
    // --------------------

    struct ggml_cgraph  * gf = ggml_new_graph(ctx);
    ggml_build_forward_expand(gf, result);

    ggml_graph_compute_with_ctx(ctx, gf, 1);

    std::vector<float> out_data(ggml_nelements(result));
    memcpy(out_data.data(), result->data, ggml_nbytes(result));
    
    ggml_free(ctx);
    return 0;
}

The simplest way to define tensors is by calling ggml_new_tensor_nd (where n can be 1, 2, 3, or 4). A complete list of tensor operator functions, such as ggml_add and ggml_mul_mat, can be found in include/ggml.h.

Understanding ggml_tensor.ne (Logical Tensor Layout)

In GGML, ne represents a tensor’s shape. It is an array of length 4, meaning GGML supports tensors with 1 to 4 dimensions, which is sufficient for most LLMs. Unused dimensions are filled with 1.

A GGML tensor’s dimension order is the reverse of PyTorch’s convention. For example, a PyTorch tensor with shape [1, 12, 64, 768] is represented in GGML as ne = [768, 64, 12, 1] . Other than that, it has exactly the same behavior as PyTorch tensor’s .shape member.

Here are some example tensor dimensions and their meanings:

[4, 3, 1, 1]: A 3×4 matrix.
[256, 256, 3, 4]: A batch of 4 RGB images, each with a resolution of 256×256 pixels.
[64, 4, 12, 1]: A GPT-2 query tensor with batch size of 1, 12 attention heads, sequence length of 4, and head dimension of 64.

Note that ne defines the tensor’s logical shape but does not represent its underlying memory layout.

Understanding ggml_tensor.nb (In-memory Tensor Layout)

In contrast to ne, which represents a tensor’s logical shape in the computational graph, nb defines how the tensor’s data is physically laid out in memory. Its values can sometimes be complex and counterintuitive.

What `nb` Represents

Each value in nb indicates the stride (i.e., the number of bytes needed to move to the next element along a given dimension). This concept may seem vague at first, so the following examples will provide a clearer understanding.

Case I: Unquantized Matrices

ggml_tensor* tensor = ggml_new_tensor_2d(ctx, GGML_TYPE_F32, 2, 6);

ne = [2, 6, 1, 1]
nb = [4, 8, 48, 48]

Interpretation:

nb[0] = 4: A float32 value takes 4 bytes.
nb[1] = 8: Moving to the next row requires 4 bytes * 2 elements per row.
nb[i] = nb[i-1] * ne[i] for higher dimensions.

Intuitive Understanding:

Dimension 0: Moving to the next float32 element requires 4 bytes.
Dimension 1: Moving to the next row requires 8 bytes.
Dimensions 2 and 3: Follow the same pattern, following the same pattern as dimension 1.

Case II: Quantized Matrices

ggml_tensor* tensor = ggml_new_tensor_2d(ctx, GGML_TYPE_Q4_0, 32, 6);

ne = [64, 6, 1, 1]
nb = [18, 36, 216, 216]

Interpretation:

nb[0] = 18: GGML’s q4_0 quantization groups 32 int4 elements together, along with one 16-bit delta value, resulting in 18 bytes per group.
At the memory level, a group of 32 elements is the smallest addressable unit, so the tensor is effectively treated as ne = [2, 6, 1, 1]with an element size of 18 bytes.
nb[i] = nb[i-1] * ne[i] for higher dimensions.

Case III: Permuted Matrices

ggml_tensor* before = ggml_new_tensor_2d(ctx, GGML_TYPE_F32, 3, 4);

// Same as PyTorch's permute()
ggml_tensor* after = ggml_permute(ctx, before, 1, 0, 2, 3);

Before Permutation:

ne = [3, 4, 1, 1], nb = [4, 12, 48, 48]

After Permutation:

ne = [4, 3, 1, 1] , nb = [12, 4, 48, 48]

Key Observation:

nb is no longer non-decreasing, as reordering dimensions can change the stride pattern.
Comment
Think of the tensor as a continuous 1D array in memory, with nb defining how indices map into it.
Comment

// Pseudo-code representation of tensor's memory layout
data = [0, 1, 2, 3 ... 11]

// Accessing row 1 before permutation, nb[0] = 4
e0 = (p + nb[0] * 0) = 0
e1 = (p + nb[0] * 1) = 1
e2 = (p + nb[0] * 2) = 2

// Accessing row 1 after permutation, nb[0] = 12
e0 = (p + nb[0] * 0) = 0
e1 = (p + nb[0] * 1) = (p + 12) = 3
e2 = (p + nb[0] * 2) = (p + 24) = 6
e3 = (p + nb[0] * 3) = (p + 24) = 6

Before permutation, the first row is [0, 1, 2], but after permutation, it becomes [0, 3, 6, 9]. Though the tensor is interpreted differently, the underlying memory layout is not affected by permutation.

One more Example for Case III: GPT-2 Self Attention Query Tensor Permutation

ggml_tensor* before = ggml_new_tensor_4d(ctx, GGML_TYPE_F32, 64, 12, 4, 1);
ggml_tensor* after = ggml_permute(ctx, before, 0, 2, 1, 3);

Before Permutation:

ne = [64, 12, 4, 1],nb = [4, 256, 3072, 12288]

After Permutation:

ne = [64, 4, 12, 1],nb = [4, 3072, 256, 12288]

Tensor Views

In some cases, allocating a unique memory block for every tensor is inefficient. Instead, GGML allows tensors to reuse memory through tensor views. Consider the following examples:

Tensor B = Tensor A + 2: Since Tensor A and B have the same shape and data type, Tensor B could reuse Tensor A’s memory block (although GGML disables in-place operations for add by default, this is just an illustrative example).
ggml_cpy(ctx, A, B): This function copies Tensor A’s data into Tensor B. Instead of allocating new memory for the result, it simply reuses B’s existing memory block.

In ggml_tensor, when a tensor does not allocate its own memory but instead references another tensor’s memory, its view_src field points to the actual memory-owning tensor.

For example, let’s take a look at the operator ggml_cpy:

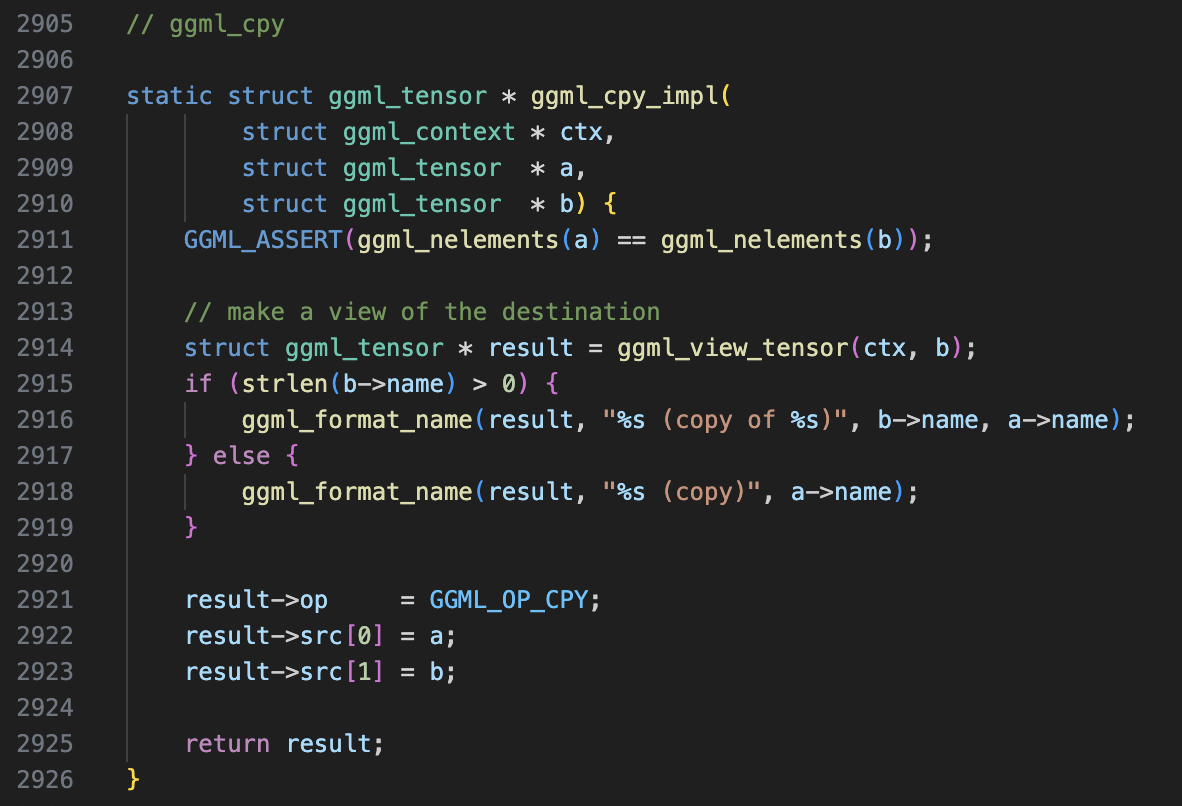
In this case, Tensor C and Tensor B share the same memory region, yet they are represented as distinct tensors in the computational graph.

Do Tensor Views Always Have the Same Shape as the Source Tensor?

No. The shape of a view tensor is always smaller than or equal to the original tensor. This means a tensor view can reference a part of another tensor rather than the entire memory block.

For example, in GPT-2 (examples/gpt-2/main-ctx.cpp), query (Q), key (K), and value (V) tensors are created using tensor views:

struct ggml_tensor* tensor_input = ggml_new_tensor_2d(ctx, GGML_TYPE_32, 768*3, seq_len);

// Create a view tensor of shape (768, seq_len) with offset 0
// The last parameter of ggml_view_2d specifies the view's offset (in bytes)
struct ggml_tensor *Qcur = ggml_view_2d(ctx0, tensor_input, 768, seq_len, cur->nb[1], 0 * sizeof(float) * 768);

// Create a view tensor of shape (768, seq_len) with offset 768
struct ggml_tensor *Kcur = ggml_view_2d(ctx0, tensor_input, 768, seq_len, cur->nb[1], 1 * sizeof(float) * 768);

// Create a view tensor of shape (768, seq_len) with offset 768 * 2
struct ggml_tensor *Vcur = ggml_view_2d(ctx0, tensor_input, 768, seq_len, cur->nb[1], 2 * sizeof(float) * 768);

Here, Q, K, and V reference different parts of the same input tensor instead of allocating separate memory blocks.

Wrapping Up

At this point, we’ve covered all the key aspects of GGML’s model inference workflow (excluding its training pipeline), I’d say the “GGML Deep Dive” series is finished for now. In upcoming posts, I’ll either (1) dive into GGML’s CUDA tensor operator implementation or (2) start a new series on llama.cpp. See you then!

Introduction#

ggml_tensor Data Structure#

Overview#

How to Setup a Simple Testing Environment#

Understanding ggml_tensor.ne (Logical Tensor Layout)#

Understanding ggml_tensor.nb (In-memory Tensor Layout)#

What nb Represents#

Case I: Unquantized Matrices#

Case II: Quantized Matrices#

Case III: Permuted Matrices#

One more Example for Case III: GPT-2 Self Attention Query Tensor Permutation#

Tensor Views#

Do Tensor Views Always Have the Same Shape as the Source Tensor?#

Wrapping Up#